UPenn ESE 680(Graph neural networks) lecture note 1 and 3

发表于 更新于 分类于

UPenn ESE 680(Graph neural networks) lecture note 1 and 3

课程目标

  1. 理解图神经网络的基础
  2. 培养利用 GNN 开发实际应用的能力

应用场景

  1. 论文作者识别：给定匿名文章推断其作者
  2. 推荐系统：预测不同客户对物品的评分
  3. 无线电资源分配
  4. etc.

NN -> CNN -> GNN

传统的神经网络无法处理多维数据，因此引入卷积操作来增强神经网络的处理能力，卷积神经网络通过堆叠多个卷积层和非线性变换层来处理数据，因此猜测图卷积神经网络也可以通过堆叠多个图卷积层和非线性变换层来达到目标，为什么会有这样的想法呢？

时间的卷积、空间的卷积和图上的卷积

我们可以利用图来处理离散的时间和空间的信号 时间信号 空间信号

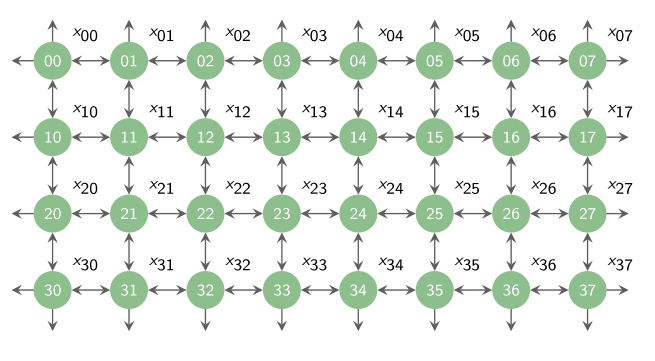
以下图为例 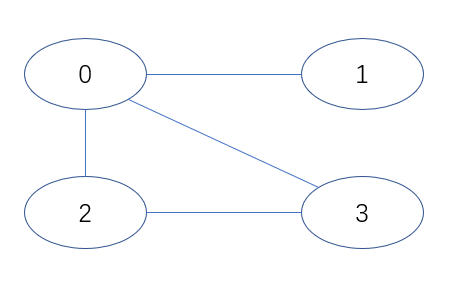图1

该图的邻接矩阵 \(A\) (adjacency matrix) 为 \[ \begin{bmatrix} 0 & 1 & 1 & 1\\ 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 1\\ 1 & 0 & 1 & 0 \end{bmatrix} \]

可以观察到 \(A = A^T\)

令 $x_i $ 为 \(N\) 维行向量，则 \(Ax_i\) 为第 \(i\) 个结点的一阶邻居 \[ \begin{bmatrix} 0 & 1 & 1 & 1\\ 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 1\\ 1 & 0 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} x_1 + x_2 + x_3 \\ x_0 \\ x_0 + x_3 \\ x_0 + x_2 \end{bmatrix} \] 可以看到每个结点都得到了它的一阶邻居的值。

同理，对于二阶邻居，只需要再乘一次邻接矩阵 \[ \begin{bmatrix} 0 & 1 & 1 & 1\\ 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 1\\ 1 & 0 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} x_1 + x_2 + x_3 \\ x_0 \\ x_0 + x_3 \\ x_0 + x_2 \end{bmatrix} = \begin{bmatrix} x_0 + x_0 + x_3 + x_0 + x_2 \\ x_1 + x_2 + x_3 \\ x_1 + x_2 + x_3 + x_0 + x_2 \\ x_1 + x_2 + x_3 + x_0 + x_3 \end{bmatrix} \] 对于每一阶邻居，给它们分别乘以一个相关系数，加起来就得到了某个结点吸收其邻居信息后的信号值 \[ Output\space z = h_0S^0x_i + h_1S^1x_i + h_2S^x_i + \cdots = \sum_{k=0}^{\infty}h_kS^kx_i \]

CNN 和 GNN 的区别

CNN 和 GNN 最大的区别在于 CNN 由于其标准的结构，其卷积层可以直接进行线性变换，而 GNN 则需要邻接矩阵吸收周围信息来进行卷积。

图位移算子 (Graph shift operator)

图位移算子就是图的矩阵表示，但是表示一个图的矩阵有很多种，我们把这些矩阵都称为图位移算子。

对于上一节的图，若图上的边带有权值，则在吸收邻居信息的时候会受权值大小的影响。

度矩阵

下面定义结点的度 (degree)，结点的度等于等于其所有边的权值的和，若为不带权的图通常将每条边的权值看作 \(1\)。对于上图，有图的度矩阵 \[ D = \begin{bmatrix} 3 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix} \] 可以看到度矩阵是一个对角阵且\(D=Diag(d_i), d_i=\sum_j{w_{ij}}\)。

拉普拉斯矩阵 (Laplacian matrix)

拉普拉斯矩阵定义为 \[ L = D - A \] 其对角线上的值为度的值，非对角线上的值为对应边的权值

正则化 (normalized) 的邻接矩阵

正则化的邻接矩阵定义为 \[ \bar{A} = D^{-1/2}AD^{-1/2} \] 即 \[ a_{ij} = \frac{w_{ij}}{\sqrt{d_id_j}} \] 若 \(A= A^T\)，则 \(\bar{A} = \bar{A}{^T}\)

正则化的拉普拉斯矩阵

正则化的拉普拉斯矩阵定义为 \[ \bar{L}=D^{-1/2}LD^{-1/2}=D^{-1/2}(D-A)D^{-1/2} = I - \bar{A} \] 即正则化的拉普拉斯和正则化的邻接矩阵是线性关系。

同样，若 \(A = A^T\)，则 \(\bar{L} = \bar{L}^{T}\)

图位移算子可以为以上任意一个矩阵

  • \(S = A\)
  • \(S = L\)
  • \(S = \bar{A}\)
  • \(S = \bar{L}\)

对于 \(S\) 具体选择哪一个则需要具体问题具体分析，但是在分析 GNN 的时候选择哪一个 \(S\) 大多数情况下不会影响我们的结果。

图信号 (Graph signal)

图信号是图上结点所携带的信息，通常为该结点的特征表示。

图信号的扩散可以定义为 \[ y = Sx \] 下图展示了图上信息的扩散过程 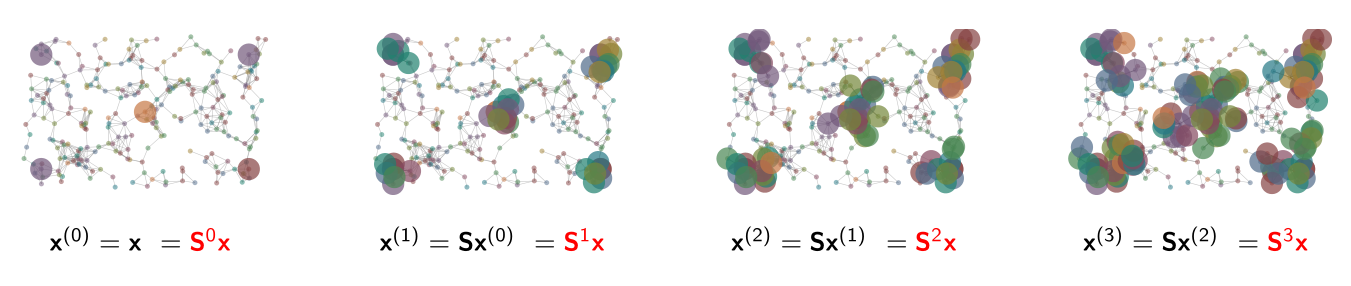图信号的扩散

要注意的是，某个结点从其他结点收集信息的过程也是其他结点进行信息扩散的过程。

图卷积过滤器 (Graph Convolutional Filters)

图卷积过滤器本质上是进行图信号线性处理的工具，给定图位移算子 \(S\) 和系数 \(h_k\)，图卷积操作可表示为多项式的和 \[ H(S) = \sum_{k=0}^{\infty}h_kS^k \] 将结果应用于图信号后可以得到 \[ y = H(S)x = \sum_{k=0}^{\infty}h_kS^kx \]

卷积过滤器 (convolutional filter) 通常定义为 \(y = h_i \star x\)

此处我们说 \(y=h_{\star S}x\) 是过滤器 \(h=\{h_k\}_{k=0}^\infty\) 在信号 \(x\) 上的图卷积结果，即 \(h\) 就是我们定义的过滤器。

经过图卷积操作，图信号邻居出发逐渐扩展至全图，实现了图信息的获得。

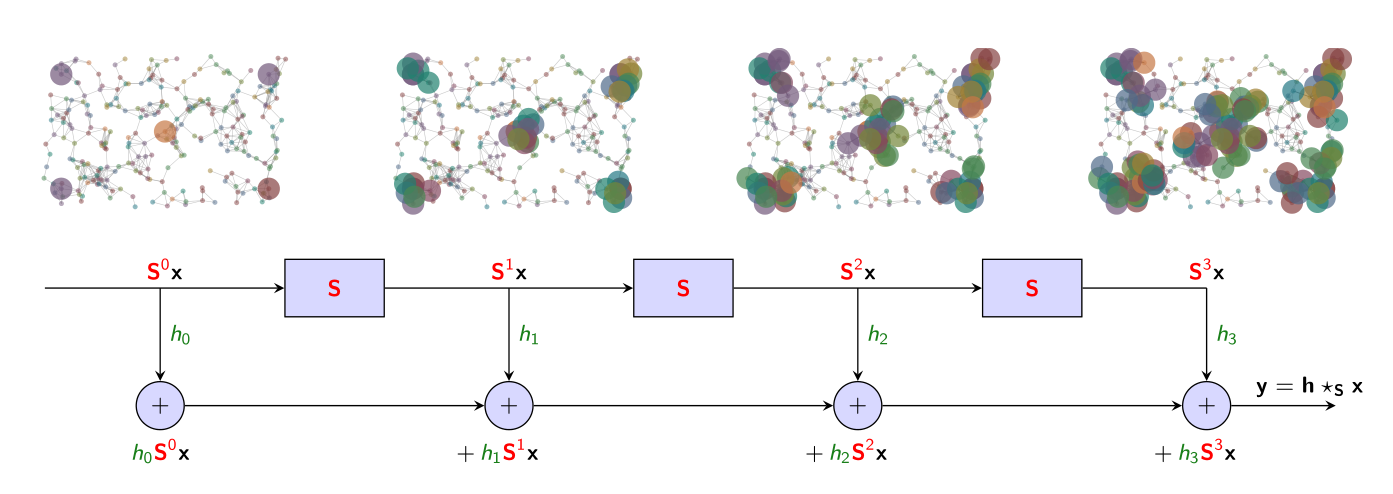
在课程中，教授将图卷积操作表示为 \[ Convolution = Shift \space . \space Scale \space . \space Sum \] Convolution

如图所示，先对信号乘以图位移算子进行 Shift 操作，随后再乘以系数进行 Scale 操作，最后将结果与上一步的结果累加起来直到结束。

图傅里叶变换 (Graph Fourier Transform)

图傅里叶变换可以将图信号从空域 (spatial domain) 转换到频域 (frequency domain)。

对于图位移算子 \(S\)， 有 \(Sv_i = \lambda_i v_i\)，其中，\(\lambda_i\) 为 \(S\) 的一个特征值， \(v_i\) 为该特征值对应的特征向量。不是一般性，我们将特征值从小到大排列，即 \[ \lambda_0 \leq \lambda_1 \leq \dots \leq \lambda_n \] 由于图位移算子 \(S\) 是实对称矩阵，所以 \(S\) 必可以正交对角化，有 \[ S = V\Lambda V^T \] 其中，\(VV^T=I\)。

现在，我们可以对图上的信号 \(x\) 定义图傅里叶变换，有 \[ \tilde{x} = V^Tx \] 该变换是在图位移算子上特征空间的投影，\(\tilde{x}\) 是 \(x\) 在图上频率的表示。

图傅里叶的逆变换定义为 \[ \tilde{\tilde{x}} = V\tilde{x} \] 注意到 \[ \tilde{\tilde{x}} = V\tilde{x} = V(V^Tx) = Ix = x \]

图过滤器对频率信号的响应

对于变换后的图信号 \(\tilde{x} = V^Tx\) 和 \(\tilde{y} = V^Ty\)，有 \[ \tilde{y} = V^Ty = V^T(\sum_{k=0}^{\infty}h_kS^kx) = V^T(\sum_{k=0}^{\infty}h_k(V\Lambda V^T)x)=\sum_{k=0}^{\infty}h_k\Lambda^k\tilde{x} \] 可以看到，对于变换后的信号，图位移算子从 \(S\) 变成了 \(S\) 的特征值 \(\Lambda\)，即对原始图信号在图过滤器上的信息扩散等价于图傅里叶变换后的信号在图过滤器的投影上的信息扩散。 \[ \tilde{h}(\lambda) = \sum_{k=0}^{\infty}h_k\Lambda^k \]

要明确扩散的方式与图无关，仅取决于算子前的系数，也就是过滤器的值，图的作用是决定进行扩散的特征值。也是因为此，我们可以在不同的图上运行同一个过滤器的值，GNN 的稳定性和可迁移性也是来源于此。

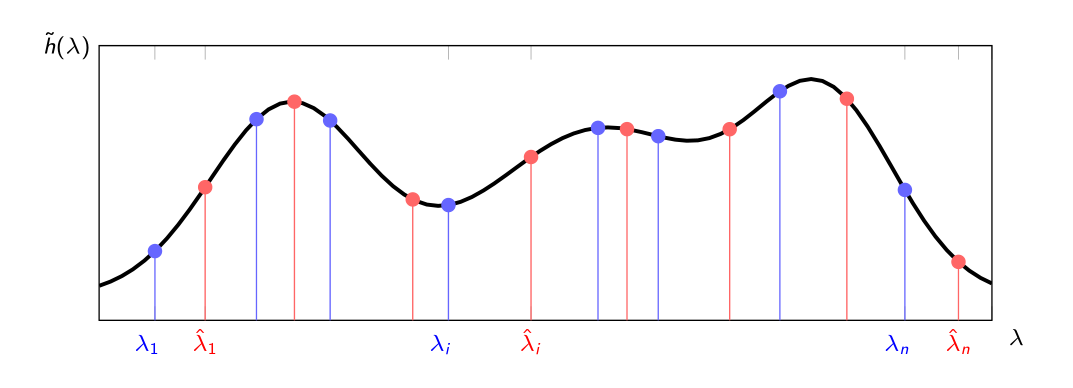同一个过滤器应用不同的特征向量 上图演示了在不同的两个图 (蓝色和红色) 上运行同一个过滤器的过程，可以看到过滤器已经固定了，对于不同的图的不同特征值，其过滤结果已经被确定了，说人话就是 \(\lambda\) 是函数 \(\tilde{h}\) 的参数，\(\tilde{h}\) 是一个具体的函数，函数的表达式被系数确定，函数的参数决定了函数最后输出什么值。

总结

这两节课讲了 GNN 运行的整个流程以及 GNN 运行中需要的参数 。

GNN 与 CNN 最大的不同就是在于卷积层的实现方式，GNN 的卷积过程被表现为图上的多次位移操作 (Shift . Scale . Sum)。在确认了对图位移算子进行多次相乘可以进行信息传递后，对图信号的转换方式开始探究，将图位移算子改为图的特征值之后，可以通过图傅里叶变换将图信号从空域转到频域，将图上的信号相互关联起来。