UPenn ESE 680(Graph neural networks) lecture note 4

图信号的学习

在图上的学习等价于图上经验风险最小化 (empirical risk minimization)，即学习 \(\Phi^\ast\)，满足 \[ \Phi^\ast = \underset{\Phi\in C}{argmin} \sum_{(x,y)\in \tau} \ell(y, \Phi (x)) \] 由上节课知识可以知道上式其实就是学习在过滤器 \(S\) 下最小损失的过滤器 \(h\) \[ h^\ast = \underset{h}{argmin} \sum_{(x,y)\in \tau} \ell(y, \Phi (x; S, h)) \] 在训练的最后一层我们需要将图信号转换成需要的数据，这一步叫做 Readout。

图神经网络的组成

课程中提到了 pointwise nonlinearity 这个用于进行非线性变化的方法，通常选择 ReLU、LeakyReLU 等对每一个元素进行变换。

对于变换函数 \(\sigma\) 将其应用于向量 \(\textbf{x}\) 的方法为 \[ \sigma[x] = \begin{bmatrix} x_1\\ x_2\\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} \sigma(x_1) \\ \sigma(x_2) \\ \vdots \\ \sigma(x_n) \end{bmatrix} \]

此时第 \(\ell\) 层的计算需要用到 \(\ell - 1\) 层的信号 \(x_{\ell - 1}\) 和过滤器 \(h_\ell = [h_{\ell0, \cdots, h_{\ell}K-1}]\)，需要注意的是，对于每一层的计算都有一个 \(h\) 来调节在信息传播过程中每一层需要获取的信息 (例如 \(h_{\ell0}\) 用来控制当前结点信号的一阶邻居的信息)。 \[ x_\ell = \sigma[\textbf{z}_\ell] = \sigma[\sum_{k=0}^{K-1}{h_{\ell k}S^kx_{\ell - 1}}] \] 对于拥有 \(L\) 层的图神经网络，每一层都有对图信号的过滤和非线性变换两部分，其中过滤是通过系数 (过滤器) \(h_{\ell k}\) 和图位移算子 \(S\) 实现的。最后的训练过程实际上只是对系数 \(h\) 进行的，\(S\) 是由图的结构确定的，作为一个先验知识引入网络中，并不进行迭代优化。

图神经网络和普通的全连接神经网络的区别在于全连接神经网络的每一层都是直接用系数 \(h\) 去和输入 \(x\) 相乘，可以将图神经网络理解为一种特殊的全连接神经网络，即和 \(x\) 相乘的系数 \(h\) 又与 \(S\) 进行了计算，因此全连接神经网络的损失相比图神经网络的损失要更小一些 \[ \underset{\mathcal{H}}{min} \sum_{(x,y)\in \tau} \ell(\Phi (x;\mathcal{H}), y) \leq \underset{\mathcal{H}}{min}\sum_{(x,y)\in \tau} \ell(\Phi (x; S, H), y) \] 但是损失增大却带来了泛化能力的提升，GNN 对于图的内部结构理解增强了其对未知信号的处理能力。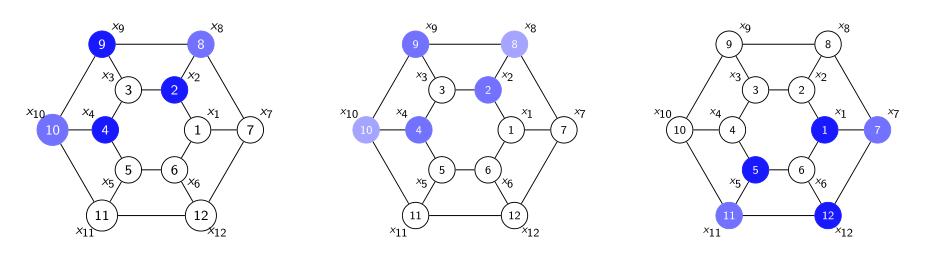

以上图为例，普通的全连接神经网络无法感知图的结构，当使用左图进行训练时，仅能对中图这种严格相同的位置信号进行预测，而图神经网络对于右图的相似的子图也能达到很好的预测效果。